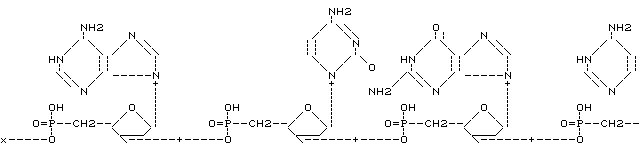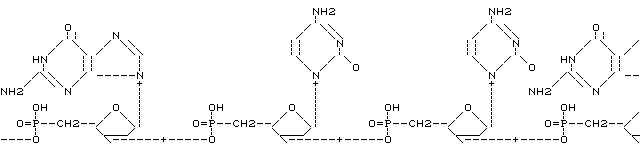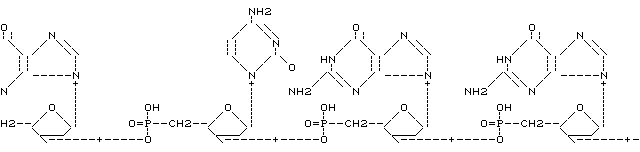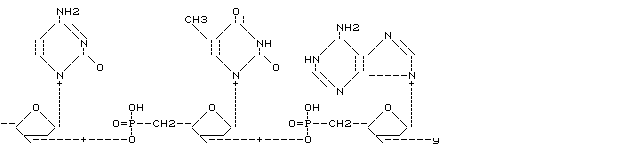
q is the quotient and r is the remainder of division of n by m. Since n-r = mq we see that n is equivalent to r, a number which may take only one of m values. For given n the remainder r after division by m is often called n mod m. The number of equivalence classes is finite, and each equivalence class is generated by the set { r+mq | q in Z}, often written r+mZ. It is possible to define addition and multiplication on the set of equivalence classes.
(x+mZ) + (y+mZ) is (x+y mod m)+mZ(x+mZ) * (y+mZ) is (x*y mod m)+mZ.
These classes are called the integers modulo m, often denoted Zm. The ring of equivalence classes is also written Z/mZ.
SWEET SIXTEEN
The values of integers are stored in a computer memory. Calculations are done with a processing unit. Most present day computers do arithmetic on the set Zm where m is a power of two. Old computers like the APPLE II had a 6502 processor which only did 8-bit arithmetic. The numbers 0-255 were divided into the numbers -127 through to 0 then 127. The value -128, represented as a byte like 10000000 was taken to be minus infinity. Normal additions and subtractions were carried out modulo 256.
Apple's technical genius, Wozniak developed sixteen bit arithmetic by software. He called this sweet sixteen. But even this system has its limitations. Numbers greater in magnitude than 32000 cause problems. The computer hardware recognises equivalence classes of numbers, rather than the numbers themselves. Five kilometers looks like five miles. NASA programmers found this out the hard way. A recent Mars module got an excessively hard landing because of this type of mistake.
SYMBOLIC MATHS
Computers cannot really do accurate arithmetic. Programmers can make the computer do arithmetic to a high precision, but there will always be problems which cannot be cracked. All the people that received erroneous bills or bank statements are fully aware of this fact. If numbers cannot be dealt with in a satisfactory manner, then why not just use the computers to sort lists of names and addresses as in 1960s style sales ledger programs ? If the computer can manipulate text strings then it should also be possible to implement math systems which deal with all of the orders of infinity invented by Georg Cantor and others.
Formal mathematics anticipated these developments in the 1930s. Church, Godel, Post and Turing contributed very much to the human achievements of the twentieth century.
Every schoolchild should have opportunity to learn a little about symbol manipulation systems. The old fashioned business of solving equations is an excercise in doing this. But solving equations often makes use of rules which may not be accurately stated. The material will seem divorced from reality to many. Time to think is important.
An equation for solution involves one or more symbols representing unknown quantities, usually numbers. If a pupil does not know how to divide, or possibly to extract square roots, then there seems little purpose in the excercise. That's where symbolic manipulation comes in.
KAMA SUTRA
To solve ax=b just write x=b/a. This is an example of a formula. Perhaps one of the best known recipes of formula is an Indian text called the Kama Sutra. It's a classical sex manual, and the literal translation is simply Love Formula. Sutra is comes from the Sanskrit root word for formula, while Kama corresponds to physical love.
Maxwell's equations are formulae connecting the electromagnetic forces, and from these come the theory of radio and television and the ability for people to watch pornographic broadcasts worldwide. The formula is the connection.
When thinking about formulae forget the calculations for a while and reach for the heavens.
If R is a ring, it is possible to add symbols to the ring so that the ring axioms R0 to R4 are satisfied. Just add the symbol X and call the new ring R[X]. The element X satisfies 1.X=X.1=1 and the value X*X is written X^2. Multiplying n copies of X is written X^n. The elements of the ring R[X] are written as sums a[0]+a[1]X+a[2]X^2 etc. with only a finite number of terms. Addition of two ring elements is done componentwise, while multiplication is achieved by collecting equal powers of X.
In the old days algebra was taught in schools by giving the pupils hundreds of excercises such as:
Multiply 1+2x+5x^5 by 3x^2+2x^3.Factorise 6x^2+5x+1.
These excercises were often chosen to avoid difficult theoretical points such as the non-existence of factors. There were often circumstances where the teachers would not have time to deal with these difficulties because of political and economic constraints. A media dominated world will see these difficulties considerably increased for the next generation of teachers.
Excercise: Verify the following identities.(1-2a)(9-4a) = 9-22a+8a^2
(3+14t)(14-11t) = 42+163t-154t^2
(12+b)(3-13b) = 36-153b-13b^2
(7c+6t)(2c+3t) = 14c^2+33ct+18t^2
(2-5t)(1-t) = 2-7t+5t^2
(-3c+4t)(-17c^2-13ct+5t^2) = 51c^3-29c^2t-67ct^2+20t^3
(15+14z)(7+5z-z^2) = 105+173z+55z^2-14z^3
(6-13a)(16+a+4a^2) = 96-202a+11a^2-52a^3
(19t-9z)(7t+18z) = 133t^2+279tz-162z^2
(13+4z)(17+19z+16z^2) = 221+315z+284z^2+64z^3
(1+t)(3-5t) = 3-2t-5t^2
(5-16c)(20+c) = 100-315c-16c^2
(7+15c)(5-17c) = 35-44c-255c^2
(9+14y)(3-21y-20y^2) = 27-147y-474y^2-280y^3
(9b+11s)(-15b+7s) = -135b^2-102bs+77s^2
(1+s)(19-6s) = 19+13s-6s^2
(17c+9s)(10c-13s) = 170c^2-131cs-117s^2
(-18c+x)(-13c^2+9cx+2x^2) = 234c^3-175c^2x-27cx^2+2x^3
(7+9y)(2+13y) = 14+109y+117y^2
(7+3s)(18+5s+11s^2) = 126+89s+92s^2+33s^3
(1-11y)(14+13y) = 14-141y-143y^2
(14-17x)(4-3x) = 56-110x+51x^2
(8+17y)(5-6y) = 40+37y-102y^2
(8-5z)(7+17z) = 56+101z-85z^2
(7c+12x)(14c+3x) = 98c^2+189cx+36x^2
(5-9b)(1-b) = 5-14b+9b^2
(11-10b)(1-6b) = 11-76b+60b^2
(18a+13y)(14a+11y) = 252a^2+380ay+143y^2
(8s+15z)(7s-9z) = 56s^2+33sz-135z^2
(-10x+y)(12x^2-4xy+13y^2) = -120x^3+52x^2y-134xy^2+13y^3
(12-7c)(5-11c) = 60-167c+77c^2
(5+9x)(10-7x) = 50+55x-63x^2
(8b-11c)(b+16c) = 8b^2+117bc-176c^2
(3+17z)(20+3z) = 60+349z+51z^2
(2-15y)(19+10y) = 38-265y-150y^2
(5c+18y)(3c+19y) = 15c^2+149cy+342y^2
(7s+t)(s+t) = 7s^2+8st+t^2
(-4b+9z)(-4b+3z) = 16b^2-48bz+27z^2
(-6t+7y)(-2t+y) = 12t^2-20ty+7y^2
(3-z)(1+z) = 3+2z-z^2
(11b+18y)(9b-y) = 99b^2+151by-18y^2
(4b+19x)(6b-x) = 24b^2+110bx-19x^2
(2-a)(14+3a) = 28-8a-3a^2
Some classical formulae attracted great controversy. The first was the formula for the area of a triangle. If A is the area of a triangle with sides a,b,c, then the quantities are related by the equation:
A^2 = s(s-a)(s-b)(s-c) where s = (a+b+c)/2.Effectively the area is given as the square root of a number. This confounded some ancient philosophers, although the formula is quite accurate and practical. The formula may be re-arranged to eliminate s. In the past students and mathematicians would use pencil and paper to do the calculations, but nowadays it can be done on the computer.
$ AOS"(a+b+c)(a+b-c)(a-b+c)(b+c-a)"-a^4+2a^2b^2+2a^2c^2-b^4+2b^2c^2-c^4
Giving 16A^2= 2(a^2b^2+a^2c^2+b^2c^2)-(a^4+b^4+c^4)
Systems such as MAPLE, MATHEMATICA, MATLAB , TK-solve and so on can do most such calculations in an instant, while the user is given time to think if using the software which should accompany these notes. Whatever the reader may think of the calculations, the symmetry of the formula should be quite evident. The values a,b,c represent the lengths of sides, or distances in space. When a=b=c it is easy to see that 16A^2=3a^4 or A= #sqrt(3/2)a^2 , where #sqrt stands for square root.
In fact the formula as written looks valid for all sets of numbers. However if a,b,c represent the lengths of a normal triangle then we know that a<=b+c and the same for the other sides. This is certainly true in Euclidean space, and also DNA space.
Two of the most famous formulae in history are:-(1) Pythagoras Theorem: a^2=b^2+c^2 for right angled triangles.
(2) Einstein's energy equation: E=mc^2.
PYTHAGORAS THEOREM
Pythagoras Theorem is easy to prove by algebra. Given a right angled triangle with sides of length a,b,c with a<=b<=c construct a square of size a+b, and fit in four triangles and a square as shown below.
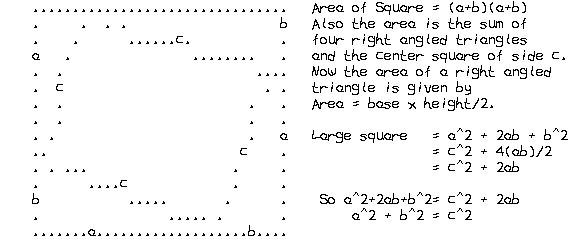 This proof is reputed to have originated in China.
This proof is reputed to have originated in China.The Triangle formula is a consequence of Pythagoras Theorem.
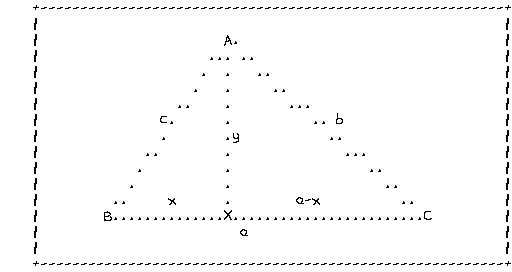
The triangle ABC may be split by drawing a perpendicular line from A to its opposite side. If the numbers a,b,c represent the lengths of the sides and x,y the distances BX and AX then we have :
Area = A = 1/2 * base * height = ay/2Pythagoras theorem can be applied to the triangles ABX and
ACX giving equations for x and y.
c^2 = x^2+y^2 (1)
b^2=(a-x)^2+y^2 (2)
It is possible to compute y in terms of a,b, and c.
Subtract (2) from (1) giving
c^2-b^2=-a^2+2ax or 2ax = a^2+c^2-b^2
For the area A the equation can be written
4A^2 = a^2y^2 = a^2(c^2-x^2)
= a^2(c^2-((a^2+c^2-b^2)/2a)^2)
16A^2 = (2ac)^2 - (a^2+c^2-b^2)^2
= (2ac+a^2+c^2-b^2)(2ac-a^2+b^2+c^2)
=((a+c)^2-b^2)(b^2-(a-c)^2)
=(a+b+c)(a-b+c)(b+c-a)(a+b-c)
RANDOM WALKS, HERD IMMUNITY AND THE LOVE BUG VIRUS
In May 2000 a Phillipino hacker released the Love Bug virus. More exactly the offending code was a 'Visual Basic Worm'. The worm was easily able to propogate amongst the computers of governments and large corporations. Following attacks on capitalism by demonstrators in Seattle, Washington, London and Chieng Mai governments and lawmakers became unduly sensitive and concentrate more forces on tracking school kids than they ever put into catching Osama Bin Laden.
The Lovebug worm is a script written in Visual Basic which is activated when users of Microsoft Outlook open e-mail attachments. An e-mail attachment is an encoded package that comes along with a plain text message. There has never been any guarantee that e-mail attachments are wholesome. Indeed many in large organisations will exchange pornographic images and suchlike. It is rumoured that the Lovebug Worm cost it's victims up to one billion dollars in lost business. The world probably benefitted because much of this so called 'business' is leading to environmental degredation and oppression of the poor. The writer, Ramel Ramirez did the world a favour.
The ease of propogation of the worm highlights the incredible stupidity of corporate fascism. The genetic sequencers promise cure for malaria or AIDS by their understanding of DNA but the industrial complex is unlikely to deliver such results quickly. What they are really seeking is loads of money immediately, and the benefits to humanity will 'trickle down' towards the poor.
Modern medicine has made vast advances in explaining immunity, but the explanations offer little consolation to individuals. What happens is that immunity works in whole populations [4]. Those who are immune to a disease act as a barrier to the propogation of the disease causing pathogen. In fact only a relatively small proportion of the population need immunity to drastically curtail disease propogation. This effect is called 'herd immunity'. Herd immunity was important in preventing the Love Bug worm doing any real harm. Users of computers whose managers were not addicted to Microsoft Office and it's cancerous overgrowths were completely unaffected.
These ideas about immunity come from physics. Boltzmann and Maxwell contributed to the kinetic theory of gases which describes the movements of gas molecules as random walks with very predictable effects for the extremely large numbers of molecules involved. This random motion of molecules can also be observed with a microscope, and is named Brownian motion after the discoverer. Temperature is related to the velocity of motion of molecules.
Mathematicians had been working on solutions of the heat equation since the 1820s. This equation and its solutions arise in areas of research ranging from the Theta Functions of Jacobi to Wall Street derivatives market.
Following the success of the kinetic theory of gases the same sorts of calculations were applied to newly discovered particles such as protons and neutrons. These calculations were particularly important in predicting the chain reactions involved in nuclear fission. Neutron absorbers and reflectors became key components in nuclear detonators.
The same models are applied to population dynamics. The modern interest in ecology and species diversity shows that people can be mobilised to express forceful views on possible absorbing and reflecting barriers in DNA space, but many of the most powerful players are sadly deficient in presentation skills. They also leave their own computer systems vulnerable to attack.
Random walk explanations start from very simple models. The first model is the simple coin tossing game with sequences of heads or tails. A sequence THHTH.... etc can be translated into motion in many different ways, but the simplest is simply counting the number of occurences of one of the faces, which is considered a success. This gives an ever increasing sequence, which can be translated into the motion of a point just moving forever in one direction at an irregular velocity.
It is possible to ask the probability that the point has moved k steps in n trials, and also where the point is most likely to be. With one trial then there is either no motion, or a displacement of one step. With probabilities of success and failure given the values p and q the number of successes S is 1 with probability p and 0 with probability q. This can be written pX+q where X is symbol. When p=q=1/2 then just write 1+X. It then happens that all the probabilities of moving k steps in n trials can be obtained by reading of the coefficients in the series (1+X)^n, dividing by a factor of 2^n. There are many proofs of this in textbooks, but the idea is to reduce statements about motion to features of polynomial multiplication. Polynomials that correspond to movement or growth are often called generating functions. What physicists did was to go and take straight limits giving things like the bell curve much loved by certain statisticians and social scientists.
Whatever the nature of the proof the theory works well in practice. Any player of backgammon or monopoly will be aware that seven is the most common total of two dice. The relative probabilities of the totals are given by reading off the coefficients of
(x+x^2+x^3+x^4+x^5+x^6)(x+x^2+x^3+x^4+x^5+x^6)x^2+2x^3+3x^4+4x^5+5x^6+6x^7+5x^8+4x^9+3x^10+2x^11+x^12
This gives seven as the most common outcome. Other features of generating functions are their ease of application. The rules don't change across different computer or language systems. As it happens genetics follows the same patterns. Going from one generation to the next various outcomes can be read off as coefficients in a polynomial. Many scientific processes are explained by taking limits of these coefficients, but DNA space is different. Just like physics has string theories, so undoubtedly we will see non-archimedian metrics applied to DNA space.
BRIDGE HANDS
In the game of Bridge each player gets 13 cards from a pack of 52. Decisions are made on point counts for high cards. The most frequently used system counts 4 for an Ace, 3 for a King, 2 for a Queen and 1 for a Jack. Zia Mahmood publicised a generating function for this point count in The Guardian.
(1+y)^36 (1+xy)^4 (1+x^2y)^4 (1+x^3y)^4 (1+x^4y)^4Zia posed a question about these distributions in his Christmas competition which is published every year in the Guardian. He got several exhaustive analyses in his responses along with correct answers on bidding and playing hands. The formula was sent by Dr Jeremy Bygott of Oxford. The coefficient of y^13 gives the generating function for point count in a 13 card hand. This is a beautiful solution.
HISTORICAL CONTEXT
Medieval times: Lords of the Array.
An array is a set of numbers arranged in lines, often called rows or columns. This meaning of the word is relatively new.
In feudal times the King could call on his vassals to provide arms and men in times of war. The managers of these mixtures of unwilling conscripts along with vain and boastful knights were called 'Lords of the Array'. The Chinese lost Hong Kong and Shanghai because they adhered to this system well into the nineteenth century. The British themselves fell victim of these feudal hangovers when a coterie of upper class generals, collectively termed 'The Donkeys' went and ordered hundreds of thousands of working class men to charge German machine gun emplacements during the First World War. These generals had learned nothing from the losses of the Chinese during the Opium wars of the 1840s and 1850s.
In the 1700s Euler investigated the problem of '36 army officers'. There are six ranks of officer, and six regiments. The idea was to arrange these officers in a 6x6 square so there were no two from either the same rank or regiment standing in line.
In 1782 Euler conjectured the problem was impossible.In 1900 G.Tarrey showed that Euler had been right through a brute force enumeration of all 6x6 latin squares.
Godement's treatise on Algebra, written in the 1960s contained tables showing the number of bombs dropped by the Americans on Viet-Nam. An excercise asked the reader to verify the associative laws of addition by adding up items in these tables.
More recently Ian Stewart described a military array problem in his regular Scientific American column [3]. The commander in chief (C-in-C) inspects his troops arranged into a certain number of squares. The C-in-C then takes his place in the army whose order of battle is a single huge phalanx, which also happens to be a square. They are unlikely to win the battle this way, but the size of the army is what counts here. The C-in-C inspects 61 equal squares of troops. The size of the army is the lowest integer solution to Y^2 = 1+61*X^2.
The equation Y^2-M*X^2=1 is known as Pell's equation. It is a perennial favourite for maths puzzles.
Excercise: Try the problem with 61 squares, then ... 9349.Excercise: For the table top.
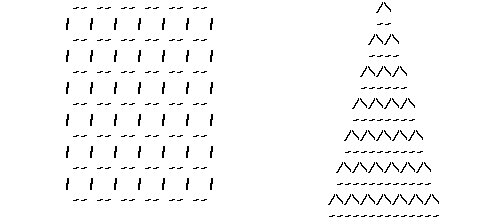 You can arrange 84 match sticks to make a 6x6 square or a set
You can arrange 84 match sticks to make a 6x6 square or a setof 28 triangles as shown. Try and make larger such arrangements.
ARRAYS IN PHYSICS
A: You are talking about physics and applied math here.
Tensors and spinors on are just special types of array which are used to explain 20th century physics. In a sense tensors are like mixtures of functions and numbers. Partial derivatives feature in many formulae involving tensors. If you are into pure maths, look at any good book on Quadratic Forms. These will give you the group theory.
REVOLUTIONARY RETRIBUTION: YEAR ZERO
Following the success of the French Revolution the new regime co-opted some of the best scientists of the day to supervise reform of the calendar. The new year was divided into months with names drawn from European folk tradition. The English made fun of this innovation by adding their own meanings. The new French years ran from September to August.
Table YEAR_ZERORevolutionary month English nick-name
Vendemiere vintage Wheezy
Brumaire mist Sneezy
Frimaire cold Freezy
Nivose snow Slippy
Pluviose rain Drippy
Ventose wind Nippy
Germinal Showery
Floreal flowers Flowery
Prairial Bowery
Messidor Wheaty
Thermidore heat Heaty
Fructidor ripening Sweety
The French calendar was worked out by a committee of experts which in included the great mathematician Laplace. Months all had the same number of days. Extra days were added between some of the months to give public holidays. Every leap year would have an extra day which could celebrate the revolution.
Laplace ensured that his role on the calendar committee was not too prominent because it bacame quite dangerous to express views for a while. Two other members of the committee went to the guillotine, and when Lavoisier the chemist was condemned his judge went on the record as saying that the revolution had no need for scientists. Nowadays Laplace is best known for Laplace's Equation which is of very great importance in electro-magnetic theory.
The extremists of the time, called Jacobins, brought in two important laws that acted as an influentual political model for the future.
(1) Law of the Suspect.Any person suspected of not giving one hundred support to the new regime could be arrested and brought before a Revolutionary Tribunal. If that person were convicted of being a counter revolutionary then there was a mandatory death sentence.
(2) Law of the maximum.The government could set maximum food prices by decree. Distributors who put up prices beyond the limit were obviously to be treated as saboteurs of the revolution.
The Jacobins also wanted to abolish torture. Their death sentences made use of the newest technology of the time: a heavy free sliding blade invented by Dr Guillotine. There is some evidence that Guillotine's technology was rather more appropriate for executions than the new fad introduced by the Americans one hundred years later. During the 1890s debates between Siemans and Westinghouse over A.C. or D.C electric power systems the Americans tried out wiring up condemned criminals to the electrodes; they are still debating this application of technology one hundred years after that. A cynic, or maybe Theodore Kaczynski, might well add that it is a pity that Laplace did not go to the guillotine as well as Lavoisier.
The Revolutionary Calendar lasted until one important date. This was the coup which saw some members of the Comittee of Public Safety gang up against Robespierre, to save their own lives. These plotters obtained the assistance of a young French army officer called Napoleon Bonepart.
It is fairly sure that Laplace was not the only astronomer who needed to be aware of the politics of the time. Most civilisations have had professional astronomers from ancient times. Some of them must have tried to get funding by predicting the fortunes of big-shots. Kepler himself is reputed to have cast a horoscope for Wallenstein, a famous European Warlord during the Thirty Years War (1618-48).
Napoleon instituted reforms in French education which are very much part of the scene today in 2010.
POLITICAL ECONOMY
Y[t+1] = Y[t]+Y[t-1]
Single population. Two cohorts.
Doubling time model. Widespread actuarial use from 1700s.
Malthus [6] popularised the idea in the 1820s.
dY/dt = K*Y
Logistic Curve. Non-linear.
dY/dt = aY-bY^2 = Y(a-bY)
Volterra Equations. 1920s Two species.
Predator and Prey.
dX/dt = aX-bXY
dY/dt = -cXY+pX
The Volterra equations remain unsolved at the time of writing. Volterra himself was directly interested in these equations. His son in law analysed statistics on the Adriatic fish catch. Population modelling has generally not received much funding. There is much commercial and political pressure to supress this sort of knowledge. Industrial fisheries are a case in point. Scientists are generally ignored when they recommend prudence while robber barons are keen to exploit the benefits of science to follow fish shoals with satellite navigation aids. In the meantime the law enforcement agencies never use high technology to catch these kleptocratic industrial pirates but turn their guns on desperate people trying to either to migrate or to ship 'illegal drugs'.
INDUSTRY AND EMPIRE
The current day meaning of a list of numbers only became common towards the end of the last century when mathematicians started a systematic study of linear equations and invented matrices, determinants and tensors. The British mathematicians, Cayley and Sylvester, were well known contributors to this field.
Ada, Countess of Lovelace [1], was an early pioneer of machine oriented calculations on arrays. One particular array taxed her mind. She worked on programming the calculation of the Bernoulli numbers, These are found in the power series expansion of cos(x)/sin(x), and x/(exp(x)-1).
Babbage had made a theoretical design of a computer to do calculations and although his computer never worked the period saw a whole lot of inventions for storing programs. These early methods included rolls of material with holes in them, or rotating drums with pins sticking out. The two methods correspond to male and female, Yin and Yang, or N and P layers of semiconductors which stand for the absence or presence of electrons.
The popular stored program machines of this era included textile machinery and clockwork music boxes. The Player Piano was perhaps the most elaborate such device. There were also early attempts to deceive the public into believing in 'chess playing computers' where the sponsor would hide a dimunitive chess master in an engine and get people to play chess against it.
AGE OF EXTREMES
Einstein needed tensors in order to construct the Theory of Relativity. From that day the 'Lords of the Array' became completely reduced to the ranks of the proletariat. Arrays and matrices were only taught in advanced maths and physics courses, and they had more theoretical than practical use. Numbers were stored by writing them on paper.
It was still easier to comission armies of manpower to handle vast calculations. Disney studios employed hundreds of artists for its animations. The Atom Bomb project used hundreds of human calculators to solve some of the differential equations.
The 'National Emergency' of the Second World War saw great advances in computing and management science. The computing community split into two with 'Partial Differential Equations' opposed to 'Commercial Data Processing'. There were those who naively believed that increased computing power could make for a better society. The idea of economic planning had been OK in wartime, and food rationing schemes had sometimes been worked out on theoretical calculations. China and Russia both had governments which paid lip service to the planned economy. Whole systems of input-output equations had been invented to describe the economy. This was often called Marxism.
Unfortunately for Soviet and Chinese statisticians these equations and the input data were too hot to handle because any data which reflected poorly on the performance of the regime would be supressed, and cause the statisticians to be imprisoned or shot.
The earliest advocates of a planned economy often had to leave their countries in order to save their own lives. Karl Popper attempts to analyse the reason for this in his book 'The Open Society and it's Enemies'. Both Stalin's Russia and Hitler's Nazi Germany embraced state planning. Thinking men voted with their feet.
CORPORATE FASCISM
Nowadays statisticians do not run such high risks of being shot. Offending data is buried in ordure. There are plenty of subservient think-tanks to produce all sorts of idiotic reports to justify government policy. Nevertheless some data is so sensitive that people will be persecuted for revealing it. Drug prices, and food and drug safety issues are jealously guarded, and there are many half forgotten cases of alleged corporate manslaughter.
Stanley Adams, a former Hoffman La-Roche employee, lost his liberty and his wife when he revealed the drug company's European price fixing arrangements. Planned profit is precious.
Also in Europe there have been several suspicious deaths of frontline data collectors in the field of vetinary medecine. The additions of hormones and antibiotics to animal feed have raised concerns about health for decades, and the agri-business sector seems to have heeded these concerns by adding good old fashioned shit to the diets of the animals.
The reader will not see many arrays in government reports, or elsewhere, including the Internet. More often reports are represented as graphs or bar charts with carefully concealed scaling information. The array that a scientist may want to access could be buried in megabytes of Post Script code.
In real life data arrays are hard to accumulate. It needs some discipline to keep figures for a time series for example. Budget cuts and privatisation are the enemies of the modern statistician. Megamergers between rival pharmaceutical companies also contribute to the chaos. Any array has an associated size, normally the number of elements in the array. This is important. Sometimes new drugs and medical treatments are advocated even though there are more doctors doing the research than patients whose treatment is being evaluated.
With the increasing power of computers it gets easier and easier to maintain statistics but most of them only reflect the enrichment of the elite: the profits of the big corporations and those of their immoral dealings which they wish to disclose to their old-boys club style regulators that run the World's capital markets. In the meantime those responsible for the data are cajoled into efficiently operating the machinary, rather than operating their brains.
THE CLASSIC CALCULATION
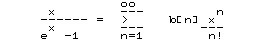
Bernoulli numbers come from from long division by power series They can be used to estimate sums by integrals. The most famous formula in which they arise is Stirling's Approximation for n factorial (n! = 1 x 2 x 3 .... x n-1 x n). Bernouilli numbers are coefficients in the expansion
x/(e^x-1) = Sum b[n]x^n/n!b[ 0]= 1 1/1
b[ 1]= -0.5 -1/2
b[ 2]= 0.16666667 1/6
b[ 4]= -0.03333333 -1/30
b[ 6]= 0.02380952 1/42
b[ 8]= -0.03333333 -1/30
b[ 10]= 0.07575758 5/66
b[ 12]= -0.25311355 -691/2730
b[ 14]= 1.1666667 7/6
b[ 16]= -7.0921569 -3617/510
b[ 18]= 54.971178 43867/798
b[ 20]= -529.12424 -174611/330
The Bernouilli numbers are calculated by inverting the series (exp(x)-1)/x. A method which minimises the use of long division is in the D4 script nm.d4f. Fast methods of computing these numbers with pencil and paper were pioneered by Ramanujan who was reputed able to do such calculations in his head. He was certainly able to calculate the first sixty or so. This was quite a feat in the days without computers, and eighty years after Babbage.
Ramanujan gave his own name to a sequence of numbers. Theses are called the Ramanujan Tau Numbers and they are the coefficients of the famous product formula:-
Delta = q * Product (1-q^2n)^24It is possible to calculate such products by repeated polynomial multiplication but it is more interesting to rearrange the product via logarithmic differentiation.
F(x) = Product (1-x^n)^klog F(x) = k * Sum log(1-x^n)
F'(x)/F(x) = k * Sum nx^n-1*(1-x^n) = A(x)
F'(x) = F(x) * A(x)
The right hand side, A(x) is a power series whose coefficients are various 'sum of divisor functions'. These coefficients can easily be determined by sieve methods and a recursion formula allows evaluation by brute force At about the same time as Ada and Babbage were struggling with the invention of the computer, a young German mathematician called Jacobi was inventing theta functions and modular forms. Jacobi arrived at some amazing identities relating power series and infinite products.
PRIME TIME
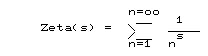 Zeta(k) is the sum 1/n^k for integers n >=0.
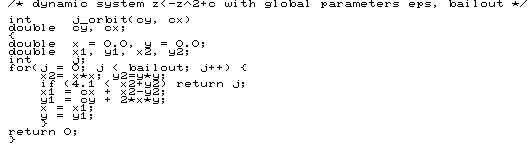
Zeta(k) is the sum 1/n^k for integers n >=0.The zeros of Zeta(s) are distributed in a T shape in the complex plane. Some are on the negative x axis, y=0, x=-2n and others are in a strip 0 The terms in the definition of Zeta(2) occur in the equations for quantum levels of spectral lines. More recently physicists have been checking resonent frequencies in dynamical systems and getting numbers that look like the distribution of the known zeros of the Zeta function. All of this work is motivated by a million dollar prize for a more precise characterisation of the zeros of the Zeta function. The Riemann hypothesis states that all the zeros not of the form s = -2n are of the form s = 1/2+it where t is real. As yet no one knows if this is true. During the search for a proof of Fermat's conjecture quite an elaborate theory of Adeles was constructed. All adeles corresponded to number fields and specialised zeta functions. These algebraic structures all had a topology and the interesting ones contained roots of unity.... solutions to X^n - 1=0. Chemists and physicists were used to working with poorly understood topologies to describe intractable results in real life. String theories are examples of weird topologies used to describe the real world. The theory of dynamical systems which gave fractals and explanations for chaos has been some advance on Galileo's theories on projectiles because it is adaptable to quantum theory. Quantum theory makes the maths of physics quite complicated if things like angles and space time co-ordinates are all integer sequences. Many states are impossible by easy calculations while other states may be subject to intractable calculations. Schrodinger's cat is either alive or dead so uncertainty is replaced by a wave function. Some very profound problems in mathematics have very simple definitions. A classic example is the '3n+1' problem or the Collatz Conjecture. For example 5 is odd so f(5)=3*5+1=16. f(16)=8, f(8)=4, f(4)=2 and f(2)=1. We also have f(1) = 4. For any function f and starting point x the sequence x, f(x), f(f(x)) .... is known as the orbit of x under f. In the case of the '3n+1' function these orbits are also known as 'Ulam Numbers'. The question concerns the eventual behaviour of such sequences: do these 'Ulam Numbers' always converge to the cycle 1 2 4 ? At the time of writing no one knows. A dynamical system is a pair (X,f) where X is a set and f is a continuous function f:X->X. For example X may be co-ordinates and momenta of sun and planets and f a rule for computing the state of the system at time t+1 given its state at time t. For any given start x[0] the sequence given by x[n+1] = f(x[n]) gives the ultimate behaviour of the system. The French mathematician Poincare invented dynamical systems. Many important problems of maths, physics and even economics and ecology can be reduced to the study of dynamical systems. Since 1986 dynamical systems have served to illustrate the limitations of mathematics as a means of predicting the real world. The simple system z<-z^2+c defined on the complex number plane is enough to generate the Mandelbrot set. The fractal images that people see are the complement of the Mandelbrot set. The colours reflect the amount of computation required to show that the iteration z<-z^2+c diverges. The fragment of C-language code generates the pixels of at the border of the Mandelbrot set. During 1984 I was working in Bangkok, Thailand. I had just completed a Thai language spreadsheet application, called 'Thai Calc' and was now working on an industrial application. Bangkok had its attractions, despite the horrendous traffic jams. The hotels which catered for Western visitors often had well stocked bookstores near to the lobbies and I would often sit in the coffee-shop of such a hotel and read an uncensored copy of the Scientific American This was a significant improvement on Saudi Arabia where the Scientific American might be available from bookstores, but often with pages cut out because of censorship. One issue contained an article by Steven Wolfram explaining 'one dimensional cellular automata'. The simplicity of the algrithm was staggering. It essentialy goes like this. For each line X[n], compute X[n+1] via the formula:- Here the integer array K represents a mapping from the set of numbers 0,1,2,... N to itself. If KEY=0 1 0 1 0 1 .... then the linear automaton represents multiplication of a polynomial by sucessive powers of 1+X+X^2 (mod 2). Other keys give remarkably complex pictures, along with many more images which just look like microscopic views of cement or concrete. Firstly I tried to program a computer to do an ASCII graphic of the evolving cells. This was easy enough with block graphic characters such as shaded rectangles and punctuation marks but as soon as I tried to display colors the program gave up. At that time I was quite keen to use ANSI escape sequences as specified in thousands of existing termcaps databases, I had access to NEC machines at the office and they all had a nice colour graphics screen. Japanese chipsets included good high resolution graphics chips at an early stage because they wanted to render their own written language in a beautiful form. By contrast the newly arrived IBM PC came with a horrible color graphic adaptor which would give the user a headache after about ten minutes. I had written a simple BASIC program to generate lines of the cellular automata, and then to add escape sequences to color individual charecters on a line of output to the screen. The escape sequences worked well on short sequences of text, or any text with only a small number of color changes. It took a considerable amount of time to find out that the program was generating the correct escape sequences, but the terminal firmware was mashing up the results because it truncated sequences if they were too long. This is typical of the computer 'bug' which fails workable programs because the program is 'too long and complicated' for the computer software to handle. This caused me to completely lose confidence in 'termcaps' style systems, and to handle screen IO via 'kitchen table' code written for each terminal, as required. Twenty five years later this 'kitchen table' stuff seems to work even better than in 1984. Back in 1984 a terminal with firmware, a screen and a keyboard cost over $1000. There were many different terminal specifications and making the same program work on all of them required a thorough understanding of termcaps. Nowdays these terminals still exist via terminal emulation and you can have six or seven running on a computer Desktop. Surprisingly development is still going on for these old fashioned terminals, and they keep on improving even on Microsoft platforms. The big impetus seems to be China, Japan and Korea or 'CJK'. The Unicode enabled 'Terminal' program on which this document is written still supports Digital Equipment VT-100 style escape sequences and I can swap colors to please my aging eyes via the same control code sequences that I learned about in 1984. The 'Linux Console' uses escape sequences. Along with UNIX and Linux came the .xpm image format used by X-windows. XPM is essentially ASCII graphics but it is supported by easily obtained programs which will convert .XPM style images to .gif or .jpg formats. Mathematics serves computers rather better than computers serve mathematics. The .jpg algorithm relies on quite sophisticated mathematics, and yet few owners of digital cameras can describe a Discrete Fourier Transform. Those people who get the 'Number Unavailable' logo on their mobile phone are unlikely to realise that a Gram-Schmit Orthogonalisation Process has failed because a matrix has become singular because it overspecifies a number of equations (one for each channel in the cell). Skills acquired through the study of mathematics tend to be more 'future proof' than other skills. That does not mean that these skills always lead people to the right conclusions. In the early 1800's many mathematicians thought they could glimpse a method of proving Fermat's Last Theorem, via unique factorisation of numbers until someone pointed out that 'unique factorisation' could not be generalised. This page is being rebuilt. The windows stuff has not been compiled since 2004, but I had it running in a Beijing cybercafe in 2008. It seems to work OK in a chinese enabled command window. The programs are in dna.exe. The use of the caret '^' for power, such as x^2 for x squared may seem to be somewhat 'tacky' or 'naff', but the search engines will find expressions entered this way. Try searching for x^2+877 next time you use a search engine.ULAM NUMBERS
f(n) = n/2 if n is even.
f(n) = 3n+1 if n is odd.
DYNAMICAL SYSTEMS

A NEW KIND OF SCIENCE
X[n+1,i] = KEY[S[i]]
REVISION NOTES
CREDITS
J. Swinnerton Dyer. A Galois Theory course.
Dr. Garling Measure Theory.
J.H.Conway For inventing 'Life'.
James Wallbank. Website hosting.
LINKS
REFERENCES
Hardy & Wright. pp19,22.
[2] n=p1+p2(=$1m).
David Ward.
The Guardian, 18 March 2000
[3] Ada and the First Computer
Eugene Eric Kim & Betty Alexandra Toole,
Scientific American, May 1999.
[4] Plagues. Their Origin, history and future.
Christopher Wills.
Harper Collins 1996.
[5] Prime Time
Erica Klarreich
New Scientist, 11 Nov 2000 #2264.
[6] An Essay on the Principle of Population
Malthus. Various editions from 1798-1830
(C) Tony Goddard, Sheffield 2011
+44(0)7944 764312
back to the top
 Chaotic roads and excessive speed.
Chaotic roads and excessive speed.